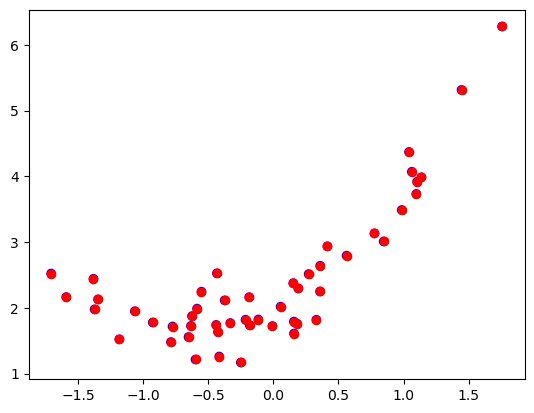
# Toy problem set of points
# After https://medium.com/towards-data-science/visualizing-gradient-descent-parameters-in-torch-332a63d1e5c5 
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(20240215)

n = 50
x = np.array(np.random.randn(n), dtype=np.float32)
y = np.array(0.75 * x**2 + 1.0 * x + 2.0 + 0.3 * np.random.randn(n), dtype=np.float32)

plt.scatter(x, y, facecolors='none', edgecolors='b')
plt.scatter(x, y, c='r')
print('Figure 1. Toy problem set of points.')
plt.show()

Figure 1. Toy problem set of points.

# ===

import torch

model = torch.nn.Linear(1, 1)
model.weight.data.fill_(6.0)
model.bias.data.fill_(-3.0)

loss_fn = torch.nn.MSELoss()
learning_rate = 0.1
epochs = 100
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

for epoch in range(epochs):
  inputs = torch.from_numpy(x).requires_grad_().reshape(-1, 1)
  labels = torch.from_numpy(y).reshape(-1, 1)

  optimizer.zero_grad()
  outputs = model(inputs)
  loss = loss_fn(outputs, labels)
  loss.backward()
  optimizer.step()
  print('epoch {}, loss {}'.format(epoch, loss.item()))

epoch 0, loss 53.078269958496094
epoch 1, loss 34.7295036315918
epoch 2, loss 22.891206741333008
epoch 3, loss 15.226042747497559
epoch 4, loss 10.242652893066406
epoch 5, loss 6.987758159637451
epoch 6, loss 4.8507561683654785
epoch 7, loss 3.4395813941955566
epoch 8, loss 2.5017752647399902
epoch 9, loss 1.8742434978485107
epoch 10, loss 1.451224684715271
epoch 11, loss 1.163843035697937
epoch 12, loss 0.9670254588127136
epoch 13, loss 0.8311155438423157
epoch 14, loss 0.7364832162857056
epoch 15, loss 0.6700497269630432
epoch 16, loss 0.6230385303497314
epoch 17, loss 0.5895166993141174
epoch 18, loss 0.5654408931732178
epoch 19, loss 0.5480331182479858
epoch 20, loss 0.5353691577911377
epoch 21, loss 0.5261048674583435
epoch 22, loss 0.5192938446998596
epoch 23, loss 0.5142641663551331
epoch 24, loss 0.5105355978012085
epoch 25, loss 0.5077620148658752
epoch 26, loss 0.5056928396224976
epoch 27, loss 0.5041452646255493
epoch 28, loss 0.5029852390289307
epoch 29, loss 0.5021142363548279
epoch 30, loss 0.5014590620994568
epoch 31, loss 0.5009655952453613
epoch 32, loss 0.5005935430526733
epoch 33, loss 0.5003127455711365
epoch 34, loss 0.5001007318496704
epoch 35, loss 0.4999404847621918
epoch 36, loss 0.49981924891471863
epoch 37, loss 0.4997275471687317
epoch 38, loss 0.49965816736221313
epoch 39, loss 0.4996056854724884
epoch 40, loss 0.49956580996513367
epoch 41, loss 0.4995356500148773
epoch 42, loss 0.4995129108428955
epoch 43, loss 0.4994955062866211
epoch 44, loss 0.4994823932647705
epoch 45, loss 0.4994724690914154
epoch 46, loss 0.49946486949920654
epoch 47, loss 0.4994591772556305
epoch 48, loss 0.49945488572120667
epoch 49, loss 0.49945151805877686
epoch 50, loss 0.49944913387298584
epoch 51, loss 0.49944716691970825
epoch 52, loss 0.49944576621055603
epoch 53, loss 0.4994446933269501
epoch 54, loss 0.4994438886642456
epoch 55, loss 0.49944329261779785
epoch 56, loss 0.4994427561759949
epoch 57, loss 0.49944236874580383
epoch 58, loss 0.49944213032722473
epoch 59, loss 0.499441921710968
epoch 60, loss 0.4994417428970337
epoch 61, loss 0.4994416832923889
epoch 62, loss 0.499441534280777
epoch 63, loss 0.4994415044784546
epoch 64, loss 0.4994415044784546
epoch 65, loss 0.49944138526916504
epoch 66, loss 0.49944132566452026
epoch 67, loss 0.49944138526916504
epoch 68, loss 0.49944138526916504
epoch 69, loss 0.49944138526916504
epoch 70, loss 0.4994412660598755
epoch 71, loss 0.4994412660598755
epoch 72, loss 0.4994412958621979
epoch 73, loss 0.4994412958621979
epoch 74, loss 0.4994412958621979
epoch 75, loss 0.4994412958621979
epoch 76, loss 0.49944132566452026
epoch 77, loss 0.4994412660598755
epoch 78, loss 0.4994412660598755
epoch 79, loss 0.4994412362575531
epoch 80, loss 0.4994412958621979
epoch 81, loss 0.4994412958621979
epoch 82, loss 0.4994412660598755
epoch 83, loss 0.4994412958621979
epoch 84, loss 0.4994412660598755
epoch 85, loss 0.4994412660598755
epoch 86, loss 0.4994412660598755
epoch 87, loss 0.4994412958621979
epoch 88, loss 0.4994412660598755
epoch 89, loss 0.4994412958621979
epoch 90, loss 0.4994412362575531
epoch 91, loss 0.4994412958621979
epoch 92, loss 0.4994412958621979
epoch 93, loss 0.4994412660598755
epoch 94, loss 0.4994412660598755
epoch 95, loss 0.4994412958621979
epoch 96, loss 0.4994412660598755
epoch 97, loss 0.4994412660598755
epoch 98, loss 0.4994412362575531
epoch 99, loss 0.4994412660598755

weight = model.weight.item()
bias = model.bias.item()
plt.scatter(x, y, facecolors='none', edgecolors='b')
plt.plot(
  [x.min(), x.max()],
  [weight * x.min() + bias, weight * x.max() + bias],
  c='r')
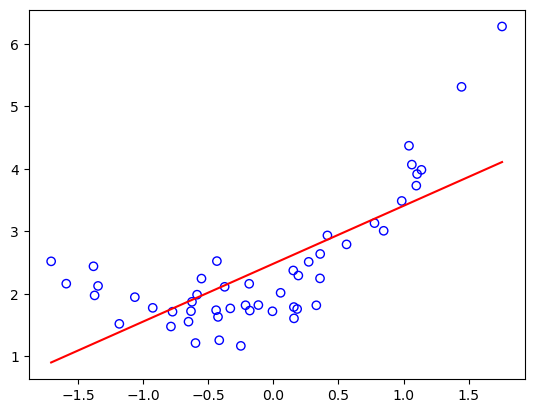
print('Figure 2. L2-learned linear boundary on toy problem.')
plt.show()

Figure 2. L2-learned linear boundary on toy problem.

# ===

def get_loss_map(loss_fn, x, y):
  """Maps the loss function on a 100-by-100 grid between (-5, -5) and (13, 13)."""
  losses = [[0.0] * 101 for _ in range(101)]
  x = torch.from_numpy(x)
  y = torch.from_numpy(y)
  for iw in range(101):
    for ib in range(101):
      w = -5.0 + 13.0 * iw / 100.0
      b = -5.0 + 13.0 * ib / 100.0

      ywb = x * w + b
      losses[iw][ib] = loss_fn(ywb, y).item()

  return list(reversed(losses))

loss_fn = torch.nn.MSELoss()
losses = get_loss_map(loss_fn, x, y)

import pylab

cm = pylab.get_cmap('terrain')
fig, ax = plt.subplots()
plt.xlabel('Bias')
plt.ylabel('Weight')
i = ax.imshow(losses, cmap=cm, interpolation='nearest', extent=[-5, 8, -5, 8])
fig.colorbar(i)
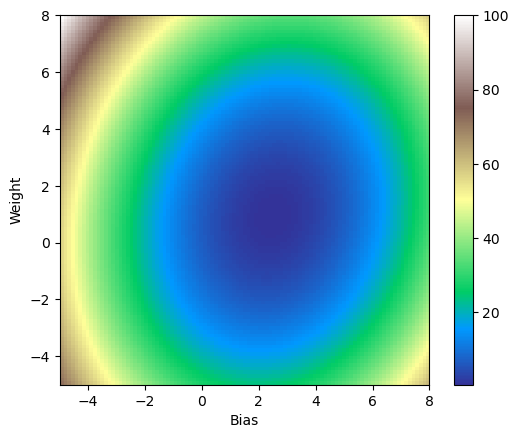
print('Figure 3. L2 loss function on toy problem.')
plt.show()

Figure 3. L2 loss function on toy problem.

# ===

model = torch.nn.Linear(1, 1)
model.weight.data.fill_(6.0)
model.bias.data.fill_(-3.0)

loss_fn = torch.nn.MSELoss()
learning_rate = 0.1
epochs = 100
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, momentum=0 * 0.9)

models = [[model.weight.item(), model.bias.item()]]
for epoch in range(epochs):
  inputs = torch.from_numpy(x).requires_grad_().reshape(-1, 1)
  labels = torch.from_numpy(y).reshape(-1, 1)

  optimizer.zero_grad()
  outputs = model(inputs)
  loss = loss_fn(outputs, labels)
  loss.backward()
  optimizer.step()
  print('epoch {}, loss {}'.format(epoch, loss.item()))
  models.append([model.weight.item(), model.bias.item()])


cm = pylab.get_cmap('terrain')
fig, ax = plt.subplots()
plt.xlabel('Bias')
plt.ylabel('Weight')
i = ax.imshow(losses, cmap=cm, interpolation='nearest', extent=[-5, 8, -5, 8])
model_weights, model_biases = zip(*models)
ax.scatter(model_biases, model_weights, c='r', marker='+')
ax.plot(model_biases, model_weights, c='r')
fig.colorbar(i)
print('Figure 4. Visualized gradient descent down loss function.')
plt.show()

epoch 0, loss 53.078269958496094
epoch 1, loss 34.7295036315918
epoch 2, loss 22.891206741333008
epoch 3, loss 15.226042747497559
epoch 4, loss 10.242652893066406
epoch 5, loss 6.987758159637451
epoch 6, loss 4.8507561683654785
epoch 7, loss 3.4395813941955566
epoch 8, loss 2.5017752647399902
epoch 9, loss 1.8742434978485107
epoch 10, loss 1.451224684715271
epoch 11, loss 1.163843035697937
epoch 12, loss 0.9670254588127136
epoch 13, loss 0.8311155438423157
epoch 14, loss 0.7364832162857056
epoch 15, loss 0.6700497269630432
epoch 16, loss 0.6230385303497314
epoch 17, loss 0.5895166993141174
epoch 18, loss 0.5654408931732178
epoch 19, loss 0.5480331182479858
epoch 20, loss 0.5353691577911377
epoch 21, loss 0.5261048674583435
epoch 22, loss 0.5192938446998596
epoch 23, loss 0.5142641663551331
epoch 24, loss 0.5105355978012085
epoch 25, loss 0.5077620148658752
epoch 26, loss 0.5056928396224976
epoch 27, loss 0.5041452646255493
epoch 28, loss 0.5029852390289307
epoch 29, loss 0.5021142363548279
epoch 30, loss 0.5014590620994568
epoch 31, loss 0.5009655952453613
epoch 32, loss 0.5005935430526733
epoch 33, loss 0.5003127455711365
epoch 34, loss 0.5001007318496704
epoch 35, loss 0.4999404847621918
epoch 36, loss 0.49981924891471863
epoch 37, loss 0.4997275471687317
epoch 38, loss 0.49965816736221313
epoch 39, loss 0.4996056854724884
epoch 40, loss 0.49956580996513367
epoch 41, loss 0.4995356500148773
epoch 42, loss 0.4995129108428955
epoch 43, loss 0.4994955062866211
epoch 44, loss 0.4994823932647705
epoch 45, loss 0.4994724690914154
epoch 46, loss 0.49946486949920654
epoch 47, loss 0.4994591772556305
epoch 48, loss 0.49945488572120667
epoch 49, loss 0.49945151805877686
epoch 50, loss 0.49944913387298584
epoch 51, loss 0.49944716691970825
epoch 52, loss 0.49944576621055603
epoch 53, loss 0.4994446933269501
epoch 54, loss 0.4994438886642456
epoch 55, loss 0.49944329261779785
epoch 56, loss 0.4994427561759949
epoch 57, loss 0.49944236874580383
epoch 58, loss 0.49944213032722473
epoch 59, loss 0.499441921710968
epoch 60, loss 0.4994417428970337
epoch 61, loss 0.4994416832923889
epoch 62, loss 0.499441534280777
epoch 63, loss 0.4994415044784546
epoch 64, loss 0.4994415044784546
epoch 65, loss 0.49944138526916504
epoch 66, loss 0.49944132566452026
epoch 67, loss 0.49944138526916504
epoch 68, loss 0.49944138526916504
epoch 69, loss 0.49944138526916504
epoch 70, loss 0.4994412660598755
epoch 71, loss 0.4994412660598755
epoch 72, loss 0.4994412958621979
epoch 73, loss 0.4994412958621979
epoch 74, loss 0.4994412958621979
epoch 75, loss 0.4994412958621979
epoch 76, loss 0.49944132566452026
epoch 77, loss 0.4994412660598755
epoch 78, loss 0.4994412660598755
epoch 79, loss 0.4994412362575531
epoch 80, loss 0.4994412958621979
epoch 81, loss 0.4994412958621979
epoch 82, loss 0.4994412660598755
epoch 83, loss 0.4994412958621979
epoch 84, loss 0.4994412660598755
epoch 85, loss 0.4994412660598755
epoch 86, loss 0.4994412660598755
epoch 87, loss 0.4994412958621979
epoch 88, loss 0.4994412660598755
epoch 89, loss 0.4994412958621979
epoch 90, loss 0.4994412362575531
epoch 91, loss 0.4994412958621979
epoch 92, loss 0.4994412958621979
epoch 93, loss 0.4994412660598755
epoch 94, loss 0.4994412660598755
epoch 95, loss 0.4994412958621979
epoch 96, loss 0.4994412660598755
epoch 97, loss 0.4994412660598755
epoch 98, loss 0.4994412362575531
epoch 99, loss 0.4994412660598755
Figure 4. Visualized gradient descent down loss function.

# ===

def learn(criterion, x, y, lr=0.1, epochs=100, momentum=0, weight_decay=0, dampening=0, nesterov=False):
  model = torch.nn.Linear(1, 1)
  model.weight.data.fill_(6.0)
  model.bias.data.fill_(-3.0)
  models = [[model.weight.item(), model.bias.item()]]

  optimizer = torch.optim.SGD(
    model.parameters(),
    lr=lr,
    momentum=momentum,
    weight_decay=weight_decay,
    dampening=dampening,
    nesterov=nesterov)
  for epoch in range(epochs):
    inputs = torch.from_numpy(x).requires_grad_().reshape(-1, 1)
    labels = torch.from_numpy(y).reshape(-1, 1)

    # Clear gradients w.r.t. parameters
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

    # print('epoch {}, loss {}'.format(epoch, loss.item()))
    models.append([model.weight.item(), model.bias.item()])

  return model, models


def multi_plot(lr=0.1, epochs=100, momentum=0, weight_decay=0, dampening=0, nesterov=False):
  fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2)
  for loss_fn, title, ax in [
    (torch.nn.MSELoss(), 'MSELoss', ax1),
    (torch.nn.L1Loss(), 'L1Loss', ax2),
    (torch.nn.HuberLoss(), 'HuberLoss', ax3),
    (torch.nn.SmoothL1Loss(), 'SmoothL1Loss', ax4),
  ]:
    losses = get_loss_map(loss_fn, x, y)
    model, models = learn(
      loss_fn, x, y, lr=lr, epochs=epochs, momentum=momentum,
      weight_decay=weight_decay, dampening=dampening, nesterov=nesterov)

    cm = pylab.get_cmap('terrain')
    i = ax.imshow(losses, cmap=cm, interpolation='nearest', extent=[-5, 8, -5, 8])
    ax.title.set_text(title)
    loss_w, loss_b = zip(*models)
    ax.scatter(loss_b, loss_w, c='r', marker='+')
    ax.plot(loss_b, loss_w, c='r')
    fig.colorbar(i)

  plt.show()

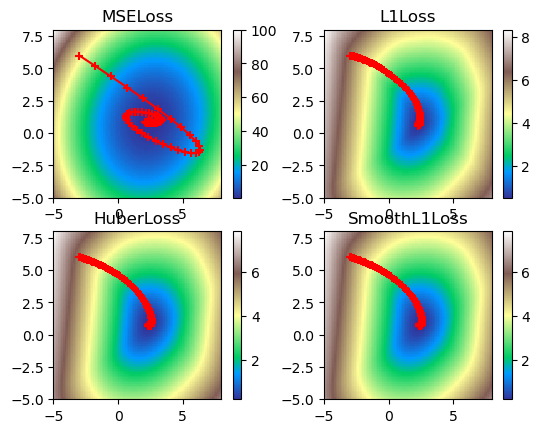
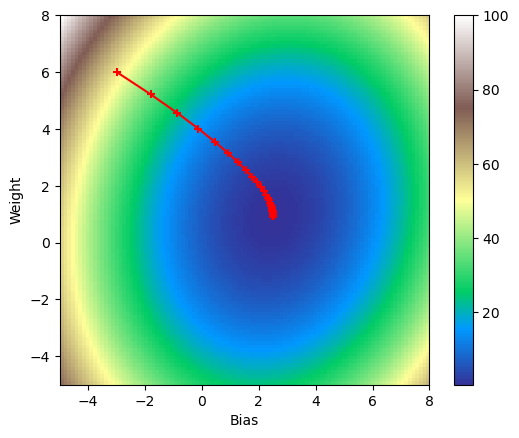
print('Figure 5. Visualized gradient descent down all loss functions.')
multi_plot(lr=0.1, epochs=100)

print('Figure 6. Visualized gradient descent down all loss functions with high momentum.')
multi_plot(lr=0.1, epochs=100, momentum=0.9)

# N.B. Figure 7 not generated by Python.

print('Figure 8. Visualized gradient descent down all loss functions with high Nesterov momentum.')
multi_plot(lr=0.1, epochs=100, momentum=0.9, nesterov=True)

print('Figure 9. Visualized gradient descent down all loss functions with high Nesterov momentum and weight decay.')
multi_plot(lr=0.1, epochs=100, momentum=0.9, nesterov=True, weight_decay=2.0)

print('Figure 10. Visualized gradient descent down all loss functions with high momentum and high dampening.')
multi_plot(lr=0.1, epochs=100, momentum=0.9, dampening=0.8)

Figure 5. Visualized gradient descent down all loss functions.

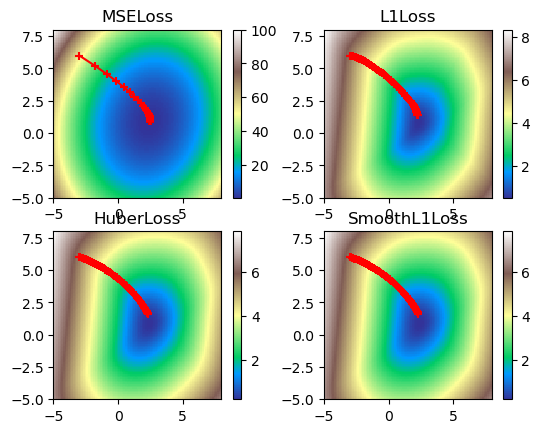
Figure 6. Visualized gradient descent down all loss functions with high momentum.

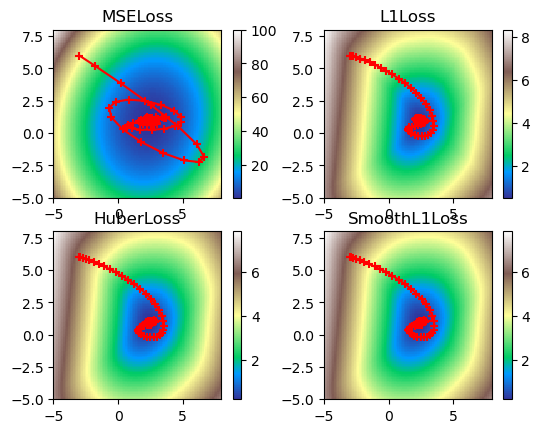
Figure 8. Visualized gradient descent down all loss functions with high Nesterov momentum.

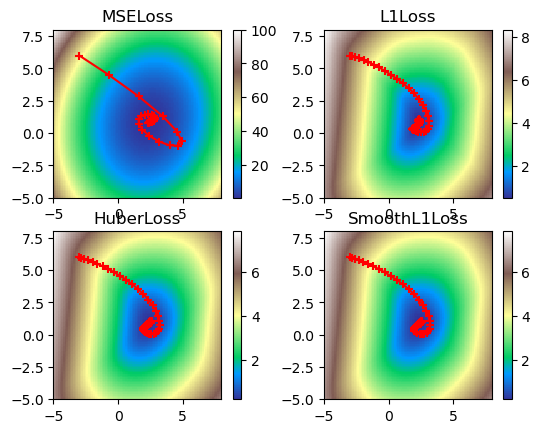
Figure 9. Visualized gradient descent down all loss functions with high Nesterov momentum and weight decay.

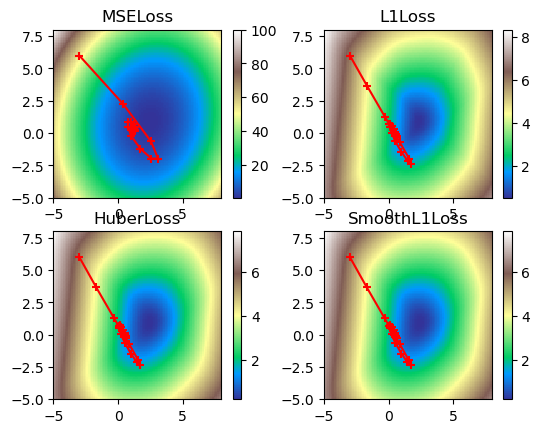
Figure 10. Visualized gradient descent down all loss functions with high momentum and high dampening.